Februari 2004
1. I en kub finns nio punkter. Visa att oavsett hur punkterna är placerade går det alltid att välja ut två som har ett avstånd från varandra som är högst hälften av rymddiagonalen.
2. Två bröder har ärvt ett inhägnat markområde som har formen av en liksidig triangel med sidlängd 100 meter. Eftersom båda gärna vill ha marken kommer de överens om att dela området i två delar med lika stor area. Den äldre brodern föreslår att de ska sätta upp ett staket från ett av triangelns hörn vinkelrätt mot motstående sida i triangeln. Den yngre brodern, som vet att staketpriset har gått upp kraftigt den senaste tiden, räknar snabbt ut att ett sådant staket skulle bli ungefär 86,6 meter långt och påstår att det räcker med ett betydligt kortare. Hur långt staket behövs egentligen för att lösa problemet?
Lösning Vinnare: Pontus Eriksson, Rudbeckianska gymnasiet, Västerås
Mars 2004
1. För vilka positiva heltal n är n! jämnt delbart med n2 ? (Talet n! ("n-fakultet") är produkten av alla heltal från 1 till n, dvs n!=1*2*3*...*n.)
2. Finns det något positivt heltal som, om det skrivs som vanligt i basen 10, blir exakt dubbelt så stort då man tar bort dess sista siffra och sätter den först? Vilket är i så fall det minsta talet med denna egenskap? Hur blir det om man använder basen 11 istället?
Lösning Vinnare: Josef Szotten, Malmö Borgarskola, Malmö
April 2004
1. Som bekant finns följande regel för att avgöra om ett positivt heltal är delbart med 9: Beräkna summan av siffrorna. Om det nya talet har mer än en siffra, så beräkna siffersumman av detta tal, och så vidare. Om det till slut blir 9, så var det tal man startade med delbart med 9, annars inte.
Här kommer ett delbarhetstest för ett annat tal. Kan du lista ut vilket?
Tag den sista siffran i talet. Fördubbla den och addera till "resten", dvs det tal som fås genom att man stryker sista siffran. Upprepa om det behövs.
Till exempel leder talet 27814 till 2781+8=2789 och vidare till 278+18=296.
2. I en likbent triangel ABC är vinklarna vid A och B 80 grader. Låt D och E vara punkter på sidorna AC respektive BC så att vinkeln ABD är 50 grader och vinkeln BAE 60 grader. Bestäm vinkeln AED.
Lösning Vinnare: Fredrik Hellman, Rudbeckianska gymnasiet, Västerås
Maj 2004
1. Bestäm de tre sista siffrorna i talet 3100 och i talet 33100.
2. Bevisa likheten
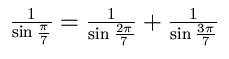
Lösning Vinnare: -
Sommaren 2004
1. Två cylindriska stearinljus är olika långa och olika tjocka. Det ena ljuset kan brinna i 4 timmar och det andra i 5 timmar. När båda ljusen har brunnit i 3 timmar är de lika långa. Vilket var det ursprungliga förhållandet mellan ljusens längder?
2. Lisa har skrivit de första tvåpotenserna på en rad:
3. Betrakta en tabell med tal. Det är tillåtet att ändra tabellen genom att byta tecken på alla tal i en rad eller en kolumn. Visa att man på det sättet kan få fram en tabell där varje radsumma och varje kolumnsumma är större än eller lika med noll.
Lösning Vinnare: Tobias Jansson, Dragonskolan, Umeå
September 2004
1. För att numrera sidorna i en 11-sidig bok från 1 till 11 går det åt 13 siffror. Finns det någon bok för vilken det går åt 2004 siffror till numreringen?
2. På ett schackbräde (8x8 rutor) sprids en "infektion". En ruta blir infekterad om den har minst två infekterade angränsande rutor (med angränsande menas här att rutorna ska ha en gemensam sida, inte bara ett gemensamt hörn). En infekterad ruta förblir alltid infekterad. Hur många rutor måste minst vara infekterade från början, om till slut alla rutor blir infekterade?
Lösning Vinnare: Annelie Östlund, Rudbeckianska gymnasiet, Västerås
Oktober 2004
1. Golvet i kung Knuts rektangulära sal är täckt med kvadratiska plattor. Salens sidlängder är sådana att det precis får plats ett helt antal plattor längs både kort- och långsidan. De plattor som ligger närmast kanterna är gula och de andra är blå. Eftersom det har bildats en hel del sprickor i plattorna under årens lopp har kungen gett Arn i uppdrag att byta ut alla plattorna mot nya av samma storlek och färg. När Arn kommer till marknaden har han glömt bort hur många plattor av varje färg som behövs. Han kommer dock ihåg att det var lika många gula som blå plattor. Han vet också att salens kortsida inte är mindre än hälften så lång som långsidan. Hjälp Arn att bestämma hur många plattor han måste köpa för att kungen ska bli nöjd!
2. Några knappar på Nisses miniräknare har gått sönder. Vissa räkneoperationer kan man dock fortfarande utföra. Det går att addera, subtrahera och invertera. Visa att man med dessa operationer fortfarande kan multiplicera två tal.
Lösning Vinnare: Robin Zenlander, Rudbeckianska gymnasiet, Västerås
November 2004
1. I en viss svensk ordlista är orden sorterade som vanligt i bokstavsordning, bortsett från att ett långt ord kommer före ett kort om de börjar likadant. T.ex. kommer ordet "femtiofyra" före ordet "femtio". Eventuella mellanslag och bindestreck bortser man från vid sorteringen. Vilket positivt heltal kommer först i denna ordlista? (Talen är skrivna på vanligt sätt, exempelvis "ett tusen fyra hundra" (inte "fjorton hundra") och "ett tusen biljoner" (inte "en miljon miljarder" eller "en biljard").)
2. I ett planetsystem med ett udda antal planeter råkar det vid ett tillfälle finnas exakt en astronom på varje planet. Om varje astronom studerar sin närmaste grannplanet, är det då möjligt att varje planet studeras av någon av astronomerna? Antag att alla distanser mellan planeterna är olika.
Lösning Vinnare: -
Jul 2004
1a. I en aritmetisk talföljd är skillnaden mellan två närliggande tal konstant. Exempelvis är följden 4, 7, 10, 13, 16, 19, ... aritmetisk med den konstanta skillnaden 3. Ge exempel på en (oändlig) aritmetisk följd av positiva heltal som inte innehåller något kvadrattal (kvadraten på ett heltal).
1b. Bevisa att om en (oändlig) aritmetisk följd av positiva heltal innehåller något kvadrattal så måste den innehålla oändligt många kvadrattal.
2. 100 passagerare har var sin biljett till 100 platser på ett flygplan. En av passagerarna är blind, och får därför gå ombord först. Eftersom han inte vet vilken plats han har, väljer han slumpmässigt en av platserna. Därefter går de övriga passagerarna ombord en i taget. Var och en sätter sig i första hand på sin plats, men om den är upptagen, väljer de slumpmässigt en av de lediga platserna. Alla slumpmässiga val görs oberoende och med lika sannolikhet för alla alternativ. Hur stor är sannolikheten att den passagerare som går ombord sist får sin plats?
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage