Februariproblemen 2004
1. I en kub finns nio punkter. Visa att oavsett hur punkterna är placerade går det alltid att välja ut två som har ett avstånd från varandra som är högst hälften av rymddiagonalen.
2. Två bröder har ärvt ett inhägnat markområde som har formen av en liksidig triangel med sidlängd 100 meter. Eftersom båda gärna vill ha marken kommer de överens om att dela området i två delar med lika stor area. Den äldre brodern föreslår att de ska sätta upp ett staket från ett av triangelns hörn vinkelrätt mot motstående sida i triangeln. Den yngre brodern, som vet att staketpriset har gått upp kraftigt den senaste tiden, räknar snabbt ut att ett sådant staket skulle bli ungefär 86,6 meter långt och påstår att det räcker med ett betydligt kortare. Hur långt staket behövs egentligen för att lösa problemet?
Lösningar
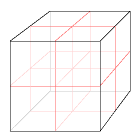
1. Dela upp kuben i åtta småkuber, som i figuren, så att alla småkuber har hälften så stor sidlängd som den stora.
/Erik
2. Arean av området är 2500*sqrt(3) (kvadratmeter), så staketet ska dela området i två delar med arean 1250*sqrt(3). (sqrt(x) betyder roten ur x.) Kortast möjliga staket får man om man sätter upp det längs en del av en cirkel med centrum i ett av triangelns hörn. (Se figur 1.) Arean av cirkelsektorn som uppstår är πr2/6, där r är cirkelns radie. För att de två delarna ska få samma area måste alltså πr2/6 = 1250*sqrt(3), vilket efter förenkling ger att r = 50*sqrt(3*sqrt(3)/π). Längden av detta staket är 2πr/6 = 50*sqrt(π/sqrt(3)), dvs ungefär 67,3 meter.
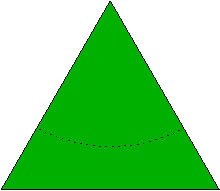 |
| Figur 1 |
För att inse att detta är optimalt använder vi den isoperimetriska olikheten, som säger att av alla områden med en viss given area så har cirkeln den kortaste omkretsen. Vi ska bevisa att hur staketet än placeras, så kan det aldrig bli kortare än i figur 1. Vi delar upp i två fall beroende på om staketet börjar och slutar på samma sida eller inte. I det första fallet tänker vi oss att vi speglar området i den sida som staketet har sina ändar på. (Se figur 2.) Staketet tillsammans med sin spegelbild innesluter då ett område med arean 2500*sqrt(3). En cirkel som har denna area måste ha radien 50*sqrt(sqrt(3)/π). Enligt isoperimetriska olikheten är denna cirkels omkrets högst lika lång som två staketlängder, så staketets längd måste i detta fall vara minst halva cirkelns omkrets, dvs 2π*50*sqrt(sqrt(3)/π)/2 ≈ 116,6.
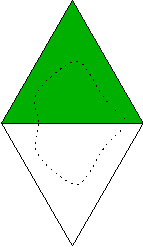 | 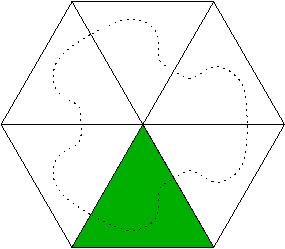 | |
| Figur 2 | Figur 3 |
Om staketet i stället börjar och slutar vid olika sidor, speglar vi området i dessa två sidor som i figur 3. De fem spegelbilderna tillsammans med staketet självt innesluter då ett område med arean 7500*sqrt(3), och en cirkel med denna area har radien r = 50*sqrt(3*sqrt(3)/π). Enligt isoperimetriska olikheten är denna cirkels omkrets högst lika lång som sex staketlängder, så staketets längd måste i detta fall vara minst en sjättedel av cirkelns omkrets, dvs 2πr/6, vilket precis är längden av staketet i figur 1. I inget fall kan alltså staketets längd vara kortare än i figur 1.
/Pontus
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage