Majproblemen 2004
1. Bestäm de tre sista siffrorna i talet 3100 och i talet 33100.
2. Bevisa likheten
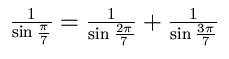
Lösningar
1. Låt oss skriva x ≡ y om de tre sista siffrorna i x och i y är lika. (Man säger att x och y är kongruenta modulo 1000.) Vi börjar med att bestämma de tre sista siffrorna i 320. 320 = (34)5 = (1+80)5 = 1 + 5*80 + 10*802 + 10*803 + 5*804 + 805, enligt formeln (a+b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5. Alla termer i summan utom de två första är delbara med 1000, så 320 ≡ 1+5*80 = 401. De tre sista siffrorna i 320 är alltså 401. Om de tre sista siffrorna i x och i y är lika, gäller detta även för heltalspotenser av x och y, dvs x ≡ y medför att xn ≡ yn för positiva heltal n. Alltså är 3100 = (320)5 ≡ (1+400)5 = 1 + 5*400 + 10*4002 + 10*4003 + 5*4004 + 4005 ≡ 1, eftersom alla termer utom den första är delbara med 1000. De tre sista siffrorna i 3100 är alltså 001.
Enligt vad vi just bevisat kan vi skriva 3100 = 1000k+1, där k är ett positivt heltal. Alltså är 33100 = 31000k+1 = (3100)10k*3 ≡ 110k*3 = 3. De tre sista siffrorna i 33100 är alltså 003.
/Pontus
2. Likheten kan visas med hjälp av addtionsreglerna för sinus och cosinus:
sin(π/7) = sin(6π/7) = 2 sin(3π/7) cos(3π/7)
sin(π/7) / sin(3π/7) = 2 cos(3π/7) = - 2 cos(4π/7) = -2
(cos2(2π/7) - sin2(2π/7) )
sin(π/7) = sin(6π/7) = sin(3 (2π/7)) = 3 cos2(2π/7) sin(2π/7) - sin3(2π/7) = sin(2π/7) ( 3 - 4 sin2(2π/7) )
sin(π/7) / sin(2π/7) + sin(π/7) / sin(3π/7) = 3 - 4
sin2(2π/7) + 2 cos(3π/7) =
= 3 - 4 sin2(2π/7) + 2 sin2(2π/7) - 2
cos2(2π/7) = 3 - 2 ( sin2(2π/7) +
cos2(2π/7) ) = 3 - 2 = 1
/Erik
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage