Aprilproblemen 2004
1. Som bekant finns följande regel för att avgöra om ett positivt heltal är delbart med 9: Beräkna summan av siffrorna. Om det nya talet har mer än en siffra, så beräkna siffersumman av detta tal, och så vidare. Om det till slut blir 9, så var det tal man startade med delbart med 9, annars inte.
Här kommer ett delbarhetstest för ett annat tal. Kan du lista ut vilket?
Tag den sista siffran i talet. Fördubbla den och addera till "resten", dvs det tal som fås genom att man stryker sista siffran. Upprepa om det behövs.
Till exempel leder talet 27814 till 2781+8=2789 och vidare till 278+18=296.
2. I en likbent triangel ABC är vinklarna vid A och B 80 grader. Låt D och E vara punkter på sidorna AC respektive BC så att vinkeln ABD är 50 grader och vinkeln BAE 60 grader. Bestäm vinkeln AED.
Lösningar
1. Om man experimenterar lite, ser man att de tal som är delbara med 19 till slut kommer till talet 19, medan de andra talen går in i en cykel som innehåller talen 1 till 18. Vi bevisar nu detta:
Vi kan skriva talet vi startar med som 10a+b, där b är slutsiffran, och a är det tal man får kvar om man stryker den. Operationen att addera två gånger slutsiffran till resten ger talet a+2b. Talet 10a+b är delbart med 19 om och endast om talet 10a+20b är delbart med 19, eftersom differensen mellan dem är 19b, en multipel av 19. Eftersom 19 saknar gemensam faktor med 10, gäller att 10a+20b är delbart med 19 om och endast om (10a+20b)/10 = a+2b är delbart med 19.
Om vi startar med ett tal som är delbart med 19, kommer alltså alla följande tal att vara delbara med 19, och omvänt, om vi startar med ett tal som inte är delbart med 19, kommer vi aldrig att få ett tal som är delbart med 19.
Om vi startar med ett tal som är större än 19, så är 9a > b, vilket innebär att 10a+b > a+2b, dvs nästa tal i följden är mindre än det tal vi startade med. Talen minskar alltså tills man får ett tal som är 19 eller mindre.
/Johan
2. Låt F vara den punkt mellan B och E som ligger på samma avstånd från A som B gör. (Se figur.)
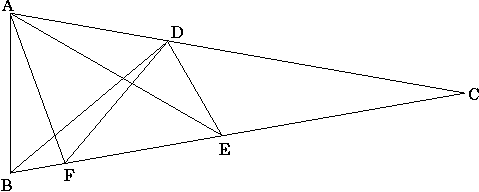
Eftersom AB=AF (AB betecknar avståndet mellan A och B) måste AFB=ABF=80. (AFB betecknar vinkeln A-F-B. Alla vinklar räknas i grader.) Vidare får vi vinklarna AEB=180-BAE-ABE=180-60-80=40, ADB=180-ABD-BAD=180-50-80=50, BAF=180-AFB-ABF=180-80-80=20 och DAF=DAB-BAF=80-20=60. Eftersom både ABD och ADB är 50 grader måste AD=AB, som ju även var lika med AF. Därför är AFD=ADF och eftersom DAF=60 måste även AFD och ADF båda vara 60 grader, dvs triangeln ADF är liksidig. Vi fortsätter nu vår vinkelberäkningsodyssé med vinklarna DFE=180-AFB-AFD=180-80-60=40 och EAF=BAE-BAF=60-20=40. Eftersom EAF=AEB måste EF=AF och eftersom triangeln ADF var liksidig är även EF=DF. Därmed följer att EDF=DEF, vinkelsumman i triangeln DEF blir EDF+DEF+DFE=2DEF+40 och för att denna vinkelsumma ska bli 180 grader måste DEF=70. Slutligen får vi nu den efterfrågade vinkeln AED=DEF-AEB=70-40=30.
/Pontus
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage