Sommarproblemen 2003
1. En kvadratisk papperslapp med sidan 6 cm viks med tre veck till en tetraeder (ej nödvändigtvis regelbunden). Hur stor volym har tetraedern?
2. De på varandra följande kvadrattalen 132 = 169 och 142 = 196 kan fås ur varandra genom att man kastar om siffrorna. Detsamma gäller 1572 = 24649 och 1582 = 24964. Visa att det inte finns tre på varandra följande kvadrattal som alla kan fås ur varandra genom omkastning av siffrorna.
3a. Visa att man med hjälp av balansvåg och 10 vikter på 1, 2, 4, 8, 16, 32, 64, 128, 256 och 512 gram kan ange vikten på alla föremål som väger mindre än ett kilo med ett fel som inte är större än 1/2 gram, om föremålet placeras i ena vågskålen och vikterna i den andra.
3b. Är det möjligt att göra samma sak med bara 9 vikter? Varför?
3c. Om man får placera vikter i båda vågskålarna, hur många vikter behövs då?
Lösningar
1. Det enda sättet att vika kvadraten till en tetraeder illustreras av figuren nedan, där P är mittpunkt till AB och Q är mittpunkt till BC. Tetraederns fyra hörn blir D, Q och P samt det hörn som bildas då A, B och C förs samman till en punkt.
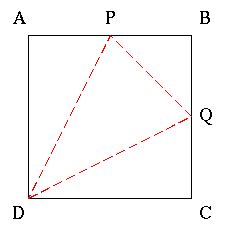
Det är lätt att bestämma tetraederns volym om man ställer den med sidan BQP som bas. Basarean är 3*3/2 = 9/2 cm2 och höjden är 6 cm, eftersom A och C är räta vinklar. Volymen är alltså
/Jonas
2. Om talet n är delbart med 3, är även n2 delbart med 3 (faktiskt till och med delbart med 9). Då är även siffersumman i talet n2 delbar med 3. Om å andra sidan n inte är delbart med 3, är siffersumman i n2 inte delbar med 3. Av tre konsekutiva kvadrattal har alltså exakt ett en siffersumma som är delbar med 3. Detta kan därför inte fås genom att man permuterar siffrorna i något av de andra två.
/Johan
3a. Eftersom vikterna är potenser av två, 20, 21, ... , 29, så kan man använda binära tal för att se vilka vikter man ska använda. Tex. 745 är 1011101001 binärt, vilket betyder att vikterna på 512g, 128g, 64g, 32g, 8g och 1g ska användas. På detta sätt kan man få fram alla tal mellan 0 och 1023 och därmed kan man ange vikten på alla föremål som väger mindre än ett kilo med ett fel som inte är större än ett 1/2 gram.
3b. Med bara 9 vikter kan man endast få fram 29=512 olika kombinationer eftersom varje vikt antingen kan användas eller inte användas. För att kunna väga med en precision på 1/2 gram krävs att det inte är mer än ett gram mellan jämförelsevikterna, så vi behöver åtminstone 1000 olika kombinationsmöjligheter.
3c. Nu har vi istället tre möjligheter för varje vikt: vänster skål, höger skål eller ingen alls. 36=729 < 1000, så 6 vikter räcker inte. 37=2187, så 7 vikter kanske fungerar? Eftersom det finns tre möjligheter väljer vi vikter som potenser av tre istället: 1g, 3g, 9g, 27g, 81g, 243g och 729g. Om vi kallar den högra vågskålen för positiv och den vänstra negativ, kan vi använda en trinär kodning, fast med decimalerna -1,0,1 istället för de vanliga 0,1,2. På så sätt kan man få fram alla vikter mellan -1093 och +1093. T.ex. 745 = 729 + 0 + 0 + 27 - 9 - 3 + 1. För att se varför man får fram alla olika tal, börja med bara en vikt på 1g, vilket ger möjligheterna -1, 0, 1. Om man också får använda 3g-vikten kan man få fram -4, -3, -2, -1, 0, 1, 2, 3, 4. Genom att fortsätta lägga till allt tyngre vikter ser man att alla tal mellan -1093 och 1093 går att uttryckas på detta sätt.
/Erik
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage