Oktoberproblemen 2003
1. Timo vill ha sitt frukostägg kokat i exakt 9 minuter. Till sitt förfogande har han två timglas. I det större tar det 7 minuter för sanden att rinna igenom och i det mindre går det på 4 minuter. Hur ska han gå till väga?
2a. Hur stor area har den största rektangel som kan skrivas in i en cirkel med radie 1?
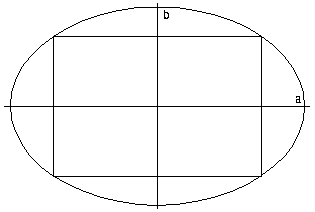
2b. Hur stor area har den största rektangel som kan skrivas in i ellipsen (x/a)2+(y/b)2 = 1 ?
Lösningar
1. Timo sätter igång båda timglasen samtidigt som ägget börjar koka. När sanden i det lilla runnit ut vänder han omedelbart på det, och när den runnit ut i det stora vänder han på det. Efter ytterligare 1 minut är sanden återigen slut i det lilla och Timo vänder då på det stora, som efter att det vänts har sand kvar för en minut. När den runnit ut har det gått 9 minuter och ägget är färdigkokt.
/Pontus
2. Flera lösningsförslag har utgått ifrån att en inskriven rektangel måste ha alla fyra hörnen på ellipsen, och sidor parallella med koordinataxlarna, dvs hörn i punkterna (x,y), (x,-y), (-x,y) och (-x,-y). Med lite derivering kan man sedan räkna ut vilka x och y som ger maximal area.
Ett sätt att angripa det här problemet, som leder till en lösning helt utan uträkningar, är att i stället bestämma den största fyrhörning som kan skrivas in i en ellips. Det visar sig nämligen att en av de maximala fyrhörningarna är en rektangel, och då måste ju denna vara en maximal rektangel.
Vi börjar med att lösa problemet för en cirkel. Om en inskriven fyrhörning ABCD har ett hörn som inte ligger lika långt från de två angränsande hörnen, t ex om B inte ligger mitt emellan A och C, kan man öka fyrhörningens area genom att flytta hörnet B till punkten B' så att bågarna AB' och B'C är lika långa. Eftersom triangeln AB'C har större area än triangeln ABC, ökar då fyrhörningens area. En maximal fyrhörning måste alltså ha egenskapen att alla sidor är lika långa, dvs den är en kvadrat. En kvadrat med diagonalen 2 har sidan roten ur 2 och arean 2.
Vi betraktar nu motsvarande problem på ellipsen (x/a)2+(y/b)2 = 1. Om vi inför de nya koordinaterna x'=x/a och y'=y/a, kommer arean av en figur i x-y-planet att vara a*b*(arean i x'-y'-planet). En maximal fyrhörning inskriven i ellipsen kommer alltså att transformeras till en kvadrat inskriven i enhetscirkeln när vi går över till koordinaterna x' och y'. Arean av en sådan fyrhörning i x-y-planet är alltså 2ab. Lägg märke till att de flesta sådana fyrhörningar inte har räta vinklar, och alltså inte är rektanglar. Om vi däremot tar en kvadrat med axelparallella sidor i x'-y'-planet, och går över till koordinaterna x och y, får vi en fyrhörning med axelparallella sidor, dvs en rektangel. Denna rektangel har den maximala arean 2ab.
/Johan
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage