Majproblemen 2003
1a. Hur många stryktipsrader måste man tippa för att vara säker på att få en rad med minst 5 rätt? En rad består som bekant av 13 matcher som ska tippas 1, X eller 2.
1b. Gör ett system med så få rader du kan som garanterar en rad med minst 6 rätt.
2. Punkten Q och den liksidiga triangeln ABC ligger i samma plan. Låt |CQ| vara längden av sträckan CQ. Bestäm det största värdet av |CQ| om |AQ| = 2 och |BQ| = 3.
Lösningar
1a. Det går med tre rader: En med bara ettor, en med bara kryss och en med bara tvåor. Eftersom det är 13 matcher måste någon av dessa ge fem rätt.
1b. 18 rader är det minsta lösning jag kan hitta som garantera sex rätt. Det är givet av dessa tre system på vardera sex rader:
|
|
|
Om vi bortser från den första helgarderade matchen, så ska vi alltså visa att oavsätt hur de resterande tolv matcherna slutar ska vi få minst 5 rätt.
Om den rätta raden har 5 eller fler lika resultat bland de 12 sista matcherna så är det inga problem, så vi antar att den består av 4 ettor, 4 kryss och 4 tvåor. Två av systemen har då 4 rätt på de 11 sista matcherna. Dessa två tillsammans ger en helgardering av match två, så något av systemen måste ge minst sex rätt.
Det är möjligt att det går att hitta ett ännu mindre system som garanterar sex rätt. Den som först hittar ett sådant belönas med ett bokpris!
/Erik
2. Då |CQ| har sitt största värde måste C och Q ligga på var sin sida om (förlängningen av) sträckan AB. Välj en punkt P så att trianglarna AQB och APC är kongruenta och orienterade som i figuren nedan, dvs med |AP| = 2 och |CP| = 3.
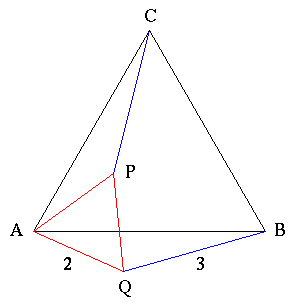
Nu måste vinkeln PAQ vara lika med vinkeln CAB som är 60o. Därmed är triangeln APQ liksidig och |PQ| = 2. Alltså är |CQ| mindre än eller lika med
med likhet då sträckorna CP och PQ har samma riktning. Eftersom vinkeln APQ är 60o inträffar detta då vinkeln APC (och vinkeln AQB) är 120o.
/Jonas
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage