Göm meny

Februariproblemen 2003

1. Ett nytt bostadsområde med höghus ska byggas och arkitekten har bestämt att våningarna ska målas i vitt och blått, dessutom får det inte vara två blåa våningar direkt ovanpå varandra. För att få lite variation får inga hus vara målade på samma sätt. Låt h(n) beteckna maximalt antal hus med n våningar. Kan du hitta en relation mellan h(n+2), h(n+1) och h(n)? Använd relationen för att beräkna hur många 16-våningshus som kan byggas!

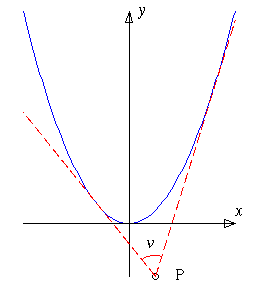
2. Andragradskurvan y = x2 betraktas från en punkt P under kurvan. Vinkeln v är den del av synfältet som upptas av kurvan (se figur). För vilka punkter P i planet är v en rät vinkel?

Lösningar

1. För små värden på n kan man beräkna h(n) genom att helt enkelt göra en lista över alla möjliga sätt att måla husen. Man finner då att h(1)=2, h(2)=3, h(3)=5, h(4)=8 och h(5)=13. Man kan utifrån detta misstänka att relationen

h(n+2) = h(n) + h(n+1)

gäller för alla n. Detta kan bevisas på följande sätt: Antag att vi ska beräkna antalet sätt att måla ett hus med n+2 våningar. Vi kan börja med att räkna antalet sätt där den första våningen är vit. Enda restriktionen är då att det inte får finnas två blåa våningar i rad bland de följande n+1 våningarna, så antalet sätt att måla ett n+2-våningshus med första våningen vit är h(n+1). Om å andra sidan den första våningen är blå, måste andra våningen vara vit, och därefter återstår n våningar av vilka inte två i rad får vara blåa. Antalet sådana hus är h(n). Detta visar att h(n+2)=h(n)+h(n+1) för alla n. Nu kan man lätt beräkna antalet möjliga 16-våningshus, genom att bilda en talföljd där varje tal är summan av de två föregående:

2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584.

Det går alltså att bygga 2584 olika 16-våningshus.

Den här talföljden, de s. k. fibonaccitalen, studerades för övrigt redan på 1200-talet av Leonardo från Pisa.

/Johan

2. Låt P ha koordinaterna (a, b). Eftersom P är under kurvan gäller  b < a2. En linje genom P har ekvationen

y = b + k(x - a),

där k är linjens riktningskoefficient. Antag nu att linjen tangerar kurvan i punkten (x, y). Då linjens och kurvans derivator är lika i tangeringspunkten följer  k = 2x. Om vi sätter in  x = k/2 och  y = x2 = (k/2)2 i linjens ekvation så får vi

(k/2)2 = b + k(k/2 - a)

eller ekvivalent

k2 - 4ak + 4b = 0.

Genom att lösa denna andragradsekvation får vi fram riktningskoefficienterna k1 och k2 för de två linjer genom P som tangerar kurvan. Då v är en rät vinkel är linjerna varandras normaler. Detta ger villkoret  k1k2 = -1. Den late löser inte andragradsekvationen, utan vet att produkten k1k2 är ekvationens konstanta term, dvs

4b = k1k2 = -1.

Därmed gäller  b = -1/4. De punkter P för vilka v är en rät vinkel ligger alltså på linjen  y = -1/4. Denna linje är också styrlinje till parabeln  y = x2.

/Jonas


Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03