Sommarproblemen 2002
1. Låt a, b, c och d vara positiva tal. Visa att minst en av följande tre olikheter måste vara falsk.
2. Vilken är den största möjliga arean av en fyrhörning med sidorna 1, 4, 7 och 8?
3. Andreas kastar en tärning ett antal gånger och antecknar varje kast på en papperslapp. Lisa tar lappen, suddar ut två godtyckliga tal x och y och antecknar istället talet (xy + x + y). Hon fortsätter med detta tills bara talet 1763 återstår. Andreas fick exakt en etta. Vad är summan av hans tärningskast?
Lösningar
1. Vi antar att alla tre olikheterna är uppfyllda. Då gäller:
= ab(a+b) + (a+b)cd < [olikhet 3]
< ab(a+b) + ab(c+d) < [olikhet 1]
< ab(c+d) + ab(c+d) = 2ab(c+d)
Det vill säga (a+b)2 < 2ab. Men
så vi får en motsägelse! Alltså kan inte alla tre olikheterna vara uppfyllda.
/Erik
2. För det första kan vi notera att den maximala arean av en fyrhörning med givna sidlängder måste antas för samtliga ordningar av sidorna. Vi kan nämligen byta plats mellan två av sidorna utan att ändra arean. I figuren nedan byter vi plats på de två övre sidorna, vilket vi kan betrakta som att triangeln ovanför den utritade diagonalen spegelvänds. Detta förändrar alltså inte arean av fyrhörningen.
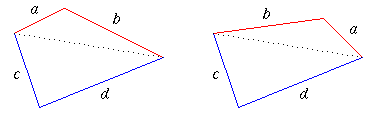
Vi kan därför anta att sidorna av längd 1 och 8 har ett gemensamt hörn, och att följaktligen även sidorna av längd 4 och 7 har ett gemensamt hörn. Om vi drar diagonalen mellan de två övriga hörnen, ser vi att arean av fyrhörningen är summan av areorna av två trianglar, varav en har två sidor av längd 1 och 8, och den andra har två sidor av längd 4 och 7.
Den maximala arean av en triangel med sidorna 1 och 8 fås om vinkeln mellan dessa sidor är rät. Arean blir då 1*8/2 = 4, och den tredje sidan får längd
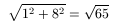
På samma sätt är den maximala arean av en triangel med två sidor av längd 4 resp 7 lika med 4*7/2 = 14, och den tredje sidan är då
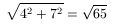
Eftersom längden av den tredje sidan blir densamma i båda fallen, är det alltså möjligt att välja vinklarna i fyrhörningen så att båda trianglarnas areor maximeras samtidigt. Fyrhörningen får då arean 4 + 14 = 18, vilket således måste vara den största möjliga arean av en fyrhörning med de givna sidlängderna.
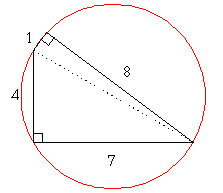
För övrigt kan nämnas att vinnaren denna omgång, David Berglund från Rudbeckianska gymnasiet i Västerås, har givit en mycket gedigen lösning på detta problem. David löser motsvarande problem för godtyckliga sidlängder, genom att härleda formeln
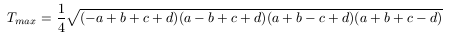
för den maximala arean av en fyrhörning med sidorna a, b, c och d. Vi presenterar inte Davids härledning här, men som David noterar, blir arean alltid maximal då vinklarna väljs så att fyrhörningen kan skrivas in i en cirkel.
/Johan
3. Vi kan beskriva den operation som Lisa utför genom att säga att hyperprodukten x^y av två tal x och y definieras som
Ett enkelt sätt att räkna ut hyperprodukten av två tal är att addera 1 till båda talen, multiplicera de två tal man då får med varandra, och slutligen dra bort 1 från produkten, dvs
Hyperprodukten är kommutativ, dvs x^y är alltid lika med y^x. Den är även associativ, dvs den uppfyller (x^y)^z = x^(y^z) för alla tal x, y och z. Båda led i ovanstående ekvation är nämligen lika med (x+1)(y+1)(z+1)-1.
Detta gör att vi utan att riskera några missförstånd kan utelämna alla parenteser i hyperprodukter av fler än två tal. En allmän formel för hyperprodukten är
Det Lisa gör när hon successivt ersätter två tal i en talföljd med deras hyperprodukt, är helt enkelt att hon räknar ut hyperprodukten av alla talen i följden. När vi har insett att hyperprodukten bara är vanlig multiplikation i förklädnad, är det också självklart att slutresultatet av Lisas beräkning inte beror på hur och i vilken ordning hon parar ihop talen. Att hyperprodukten av talen är 1763 innebär att om vi adderar 1 till alla tärningskasten, blir den vanliga produkten av dessa tal 1764.
Vi undersöker därför på vilka sätt 1764 kan skrivas som en produkt av tal från 2 till 7. 1764 har primfaktoriseringen 2*2*3*3*7*7. Vi kan här ersätta två tvåor med en fyra, eller en tvåa och en trea med en sexa, och fortfarande ha tal från 2 till 7. Vi får alltså följande möjligheter:
De tärningskast Lisa startade med måste därför ha varit en permutation av någon av följderna (1,1,2,2,6,6), (2,2,3,6,6), (1,2,5,6,6) och (5,5,6,6). Att det fanns exakt en etta i följden innebär att talen måste ha varit 1, 2, 5, 6 och 6, och att summan följaktligen var 20.
/Johan
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage