Septemberproblemen 2002
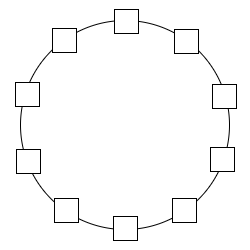
1. Går det att placera ut talen 1 till 10 i de tomma rutorna runt
cirkeln, så att summan av tre rutor i följd alltid är mindre än eller lika med
16? Ge exempel eller förklara varför det inte går!
Går det om man även
tillåter summan 17? 18?
2. Ett tredimensionellt luffarschack består av 64 kulor arrangerade som en kub (4x4x4). Hur många olika rader om fyra kulor kan man hitta i kuben?
Lösningar
1. Det här problemet kan lösas med ett så kallat probabilistiskt resonemang. Märkligt nog kan man nämligen ibland använda sannolikhetsteori för att komma till helt säkra slutsatser även om sådant som inte i sig innehåller något slumpmässigt element.
Vi tänker oss att talen 1-10 har skrivits runt cirkeln. Vi väljer sedan slumpmässigt tre konsekutiva tal, på så sätt att alla tio sätten att göra detta har sannolikhet 1/10. Vad är då väntevärdet (det genomsnittliga värdet) av summan av de tre talen? Eftersom varje tal, oavsett var det står och vilka grannar det har, kommer att finnas med i summan med sannolikhet 3/10, är väntevärdet av summan lika med (3/10)*(1+2+3+4+5+6+7+8+9+10) = 16.5.
Poängen är att detta värde är oberoende av hur talen har placerats ut. Vi vet inte vilka summor som förekommer, eller exakt vilka sannolikheter dessa har, men eftersom väntevärdet är större än 16, måste minst en summa av tre konsekutiva tal vara större än 16, dvs minst 17.
Går det att placera ut talen så att största summan är 17? Om vi låter ett "fönster" som rymmer tre rutor glida längs cirkeln, ser man att det som händer när fönstret flyttas ett steg är att en ruta byts ut mot en annan ruta tre steg bort. Det innebär för det första att varje gång man flyttar fönstret ett steg, kommer summan av de tre talen i fönstret att ändras. Samma summa kan därför inte förekomma på mer än fem ställen längs cirkeln. För det andra kan vi konstatera att differensen mellan den största och den minsta summan måste vara minst 2. Om vi nämligen letar rätt på talet 1, måste vi finna att av de två tal som står tre steg medsols respektive motsols från denna ruta, är minst ett större än eller lika med 3.
Om vi antar att den största summan är 17, kan alltså värdet 17 förekomma högst fem gånger, samtidigt som någon summa måste vara mindre än eller lika med 15. Väntevärdet av en slumpmässigt vald summa kan då vara högst (5*17+4*16+15)/10 = 16.4. Eftersom väntevärdet alltid är 16.5, är detta en motsägelse. Den största summan måste alltså vara minst 18.
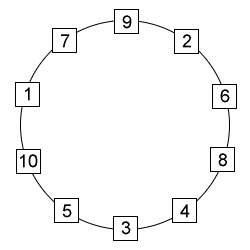
Att det är möjligt att placera ut talen så att ingen summa överstiger 18 framgår av nedanstående figur:
Hur kommer det sig att en darttavla ser ut som den gör? Klicka här.
/Johan
2. Problemet är ekvivalent med att hitta antalet linjer som skär exakt fyra punkter i ett tredimensionellt punktgitter med 4*4*4 punkter. Men låt oss börja i två dimensioner för att se mönstret. I ett gitter med 4*4 punkter finns det 10 linjer som skär exakt fyra punkter, 8 linjer parallella med någon kant och 2 diagonaler.
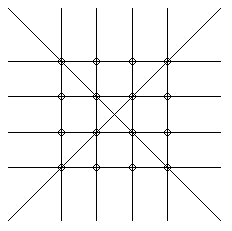
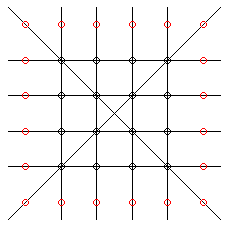
Om vi nu ritar ett gitter med 6*6 punkter ser vi att de inre punkterna är ett gitter med 4*4 punkter. De yttre (röda) punkterna är 62-42 = 20 till antalet. Varje linje skär två yttre punkter och genom varje yttre punkt går exakt en linje. Därmed är antalet linjer lika med hälften av antalet yttre punkter, dvs 10 stycken.
På samma sätt i tre dimensioner. Vårt gitter med 43 punkter är inre punkter i ett gitter med 63 punkter. Varje linje som skär fyra punkter i det inre gittret skär också två yttre punkter och genom varje yttre punkt går exakt en sådan linje. Så antalet linjer är också i detta fall hälften av antalet yttre punkter i det stora gittret, dvs
Av dessa 76 linjer är 48 parallella med någon kant, 24 diagonala men parallella med någon sida samt 4 rymddiagonala.
Generellt: Antalet linjer som skär N punkter i ett D-dimensionellt gitter med ND punkter är
/Jonas
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage