Göm meny

Marsproblemen 2002

1. Med hur många nollor avslutas talet  2002! = 1*2*3*...*2002 ?

2. Till varje sida i en triangel hör en höjd - den höjd triangeln får om sidan väljs som bas. I en viss triangel är bara en av sidorna längre än sin höjd. Bestäm triangelns vinklar.

Lösningar

1. För att finna hur många nollor talet 2002! avslutas med ska vi räkna ut hur många gånger vi kan dela det med 10 = 2*5. Faktorn 2 finns betydligt fler av än faktorn 5, så det är antalet primfaktorer 5 i 2002! som kommer ge vårt svar.

  • Talen 5, 10, 15, ..., 2000 är delbara med 5, dvs 2000/5 = 400 tal bidrar med minst en faktor 5.
  • Talen 25, 50, 75, ..., 2000 är delbara med 25 = 5*5, dvs 2000/25 = 80 tal bidrar med ytterligare minst en faktor 5.
  • Talen 125, 250, 375, ..., 2000 är delbara med 125 = 5*5*5, dvs 2000/125 = 16 tal bidrar med ytterligare minst en faktor 5.
  • Talen 625, 1250, 1875 är delbara med 625 = 5*5*5*5 och bidrar med ytterligare en faktor 5.

Sammanlagt får vi alltså 400+80+16+3 = 499 faktorer 5. Antalet faktorer 2 är minst 2002/2 = 1001 > 499 (alla jämna tal är delbara med 2), så vi får att 2002! avslutas med 499 nollor.

/Erik

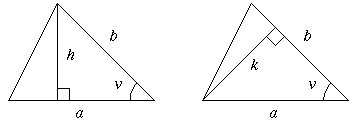
2. Låt a och b vara de sidor som inte är längre än sina respektive höjder och låt v vara vinkeln mellan dessa sidor. Låt vidare h vara höjden mot a och k vara höjden mot b (se figuren nedan).

Låt "<=" betyda "mindre än eller lika med". Enligt vårt antagande gäller

a <= h   och   b <= k.

Ur figuren får vi

sin(v) = h/b = k/a <= 1.

Sammantaget ger det oss olikheterna

a <= h <= b <= k <= a.

Men här måste vi ha likhet i varje led, eftersom en sträng olikhet i något led skulle medföra a < a. Därmed gäller a = h = b = k och sin(v) = 1, så att v = 90o. Triangeln är alltså likbent och rätvinklig med vinklarna 90o, 45o och 45o.

/Jonas


Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03