Linköpings Universitet

Julproblemen 2003

1. Lisa säger till Nisse: "Det blir soligt i morgon, jag slår vad om att Kalle tänker tvätta bilen." Nisse, som vet att Kalle tvättar sin Peugeot exakt tre gånger varje vecka, svarar: "OK, hur mycket satsar du?" De kommer överens om att Lisa ska starta med 100 kronor, och varje morgon under en vecka får hon satsa ett valfritt belopp på att Kalle kommer att tvätta bilen den dagen. Om det stämmer, vinner hon lika mycket som hon har satsat, annars förlorar hon insatsen. Nisse tänker att eftersom Kalle tvättar bilen tre dagar i veckan, men låter bli fyra dagar i veckan, borde han ha större chanser att vinna. Lisa vet också att Kalle tvättar bilen exakt tre gånger i veckan. Hon inser att hon kan utnyttja den information hon får efter hand för att bestämma sin insats dag för dag.

Finns det någon strategi som gör att Lisa kan vara säker på att sluta med mer än 100 kronor? Hur stor vinst kan hon garantera i värsta fall, och hur mycket ska hon då satsa första dagen?

2. Några personer möts på ett café och börjar diskutera vilka av dem som träffats vid något tidigare tillfälle. Det visade sig att om man väljer ut tre av dem, så är det alltid några av dessa tre som mötts innan och dessutom är det alltid några av dem som inte träffats tidigare.

Hur många personer kan det högst ha varit?

---

Lösningar

1. Lisa kan satsa så att hon är säker på att sluta med minst 129 kronor. Hur det går till framgår av nedanstående schema. Hon börjar i övre vänstra hörnet. När hon vinner går hon åt höger, och när hon förlorar går hon nedåt. Hur mycket hon ska satsa i varje steg framgår. T ex ska hon efter första dagen ha 115 kronor om hon vinner, och 85 kronor om hon förlorar, dvs hon ska satsa 15 kronor.

100	→	115	→	125	→	129
↓		↓		↓
85	→	105	→	121	→	129
↓		↓		↓
65	→	89	→	113	→	129
↓		↓		↓
41	→	65	→	97	→	129
↓		↓		↓
17	→	33	→	65	→	129

Att 129 kronor är det bästa man kan garantera är litet svårare att bevisa. Ett sätt är att försöka fylla i en tabell som den ovan, men med 130 i stället för 129 i den högra kolumnen. Om man konstruerar tabellen från höger till vänster och nedifrån upp, och hela tiden väljer så små tal som möjligt, kommer man att få ett tal större än 100 i övre vänstra hörnet, vilket visar att man skulle behöva starta med mer än 100 kronor för att vara säker på att sluta med minst 130.

Ett annat sätt är följande: Antag att Lisa har en strategi som gör att hon alltid slutar på minst 130 kronor. Vi ska visa att detta leder till en motsägelse. Vi modifierar därför situationen så att Kalle varje dag singlar slant för att avgöra om han ska tvätta bilen eller inte (dvs villkoret att han tvättar den exakt tre gånger är inte längre uppfyllt). Vi låter Lisa använda sin strategi i denna situation. Eftersom Lisa inte satsar någonting om Kalle redan har tvättat bilen tre gånger, kommer resultatet då att bli att hon slutar på minst 130 kronor om Kalle tvättar bilen minst tre gånger. Det finns 2⁷ = 128 olika utfall av slantsinglingarna, och 99 av dessa leder till att Kalle tvättar bilen minst tre gånger. Sannolikheten för detta är alltså 99/128. Lisa kommer alltså i genomsnitt att sluta med minst 130*99/128 kronor. Emellertid kommer hon, oavsett hur bra eller dåligt hon satsar, alltid att ha i genomsnitt 100 kronor! Detta beror på att det nu är slantsinglingarna som avgör om Lisa vinner eller förlorar. Även om hon låter sin insats bestämmas av vad som har hänt tidigare i veckan, har hon varje dag exakt 50% chans att vinna. Eftersom 130*99/128 > 100, har vi en motsägelse. Det finns alltså ingen strategi som garanterar 130 kronor.

/Johan

---

2. Det går med fem personer, men inte fler. Figur 1 illustrerar att det fungerar med fem personer, svart linje betyder att de känner varandra och röd att de inte känner varandra. Om man studerar figuren ser man att det inte finns tre personer där alla tre linjerna mellan dem har samma färg, så villkoret är uppfyllt.

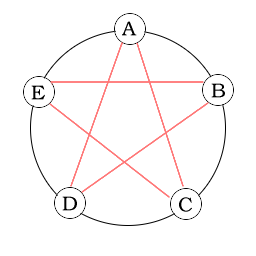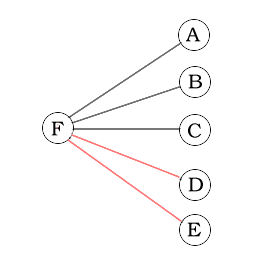Figur 1	Figur 2

Om de är sex personer går det däremot alltid att hitta tre personer där antingen alla känner varandra eller inga känner varandra. Vi börjar med att undersöka person F, se figur 2. Eftersom det finns fem andra måste aningen F känna tre personer, eller vara obekant med tre personer. Vi kan anta att det förstnämnda är sant (det andra fallet blir likadant, fast med färgerna ombytta), och kallar dem som F känner för A, B och C.

Om nu två av A, B och C känner varandra får vi att F tillsammans med dessa två alla känner varandra. I annat fall är A, B och C alla obekanta.

Om ni är intresserade av mer information om problem av den här typen, läs om Ramseytal hos mathworld.com.

/Erik

Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03