Oktoberproblemen 2002
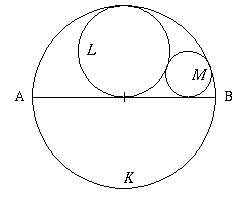
1. Låt sträckan AB vara en diameter till en cirkel K. Cirkeln L tangerar K och mittpunkten på AB. Cirkeln M tangerar K, L och AB. Bestäm kvoten mellan K:s area och M:s area!
2. Svante ska rita ett rutnät med 10 x 10 rutor. Han använder ett ritprogram där man kan rita rektanglar genom att klicka på två motstående hörn. Hur många rektanglar måste han rita för att få ett fullständigt rutnät? Testa nedan genom att klicka på punkterna! Kan du bevisa att den lösning du hittar är optimal?
Lösningar
1. Antag för enkelhets skull att K har radie 1, så att L får radie 1/2. Låt L ha medelpunkt P och tangera diametern AB i punkten S. Punkten S är alltså medelpunkt för K. Låt vidare M ha medelpunkt Q och tangera AB i punkten T. Kalla radien av M för x. Låt slutligen R vara den punkt på sträckan SP som uppfyller |SR| = |TQ| = x.
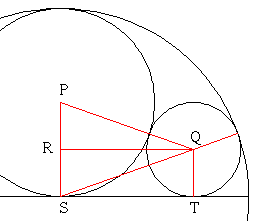
Pythagoras sats för triangeln SRQ:
Pythagoras sats för triangeln PRQ:
Därmed gäller ekvationen 1 - 2x = 2x, som har lösningen x = 1/4. Kvoten mellan cirklarnas areaor är alltså 12/x2 = 16.
Frida Herrgård, Rudbeckianska gymnasiet, Västerås visar på ett mycket elegant sätt att x = 1/4 är en lösning till problemet. Frida visar inte hur man kommer fram till just x = 1/4, men eftersom problemet inte kan ha mer än en lösning så är inte det nödvändigt. Fridas idé kan beskrivas som följer:
Rita den stora cirkeln K och diametern AB. Rita därefter fyra cirklar med radie 1/4 som alla tangerar AB och K på insidan. Kalla en av dessa små cirklar för M. Rita därefter en cirkel I med radie 1/2 och samma medelpunkt som K. Cirkeln I måste då tangera de små cirklarna. Drag en linje parallell med AB genom M:s medelpunkt och spegla I i denna linje. Kalla spegelbilden för L.
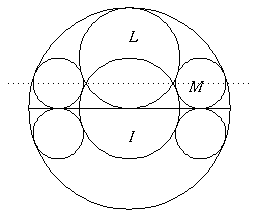
Det är lätt att verifiera att cirklarna M och L som konstruerats på detta sätt uppfyller alla förutsättningar i problemet. Därmed är x = 1/4 en lösning.
/Jonas
2. Om man experimenterar lite, ser man ganska snabbt att det är möjligt att åstadkomma ett fullständigt rutnät med 11 rektanglar. Detta kan göras på många sätt. Till exempel kan man börja med att rita ramen, dvs den maximala 10x10-rektangeln. Sedan kan man åstadkomma de nio horisontella linjerna som återstår med fem stycken 1x10-rektanglar, och de nio vertikala linjerna som återstår med fem 10x1-rektanglar.
Att bevisa att 11 rektanglar är optimalt, dvs att det inte finns någon lösning med bara 10 rektanglar, är däremot ganska knepigt. Själv har jag kommit på följande lösning:
Vi börjar med att visa att man behöver minst 10 rektanglar. Vi gör detta genom att tilldela varje linjesegment som förbinder två intilliggande gitterpunkter ett visst poängvärde. De linjesegment som går från en punkt på en sida av 10x10-kvadraten, och in i det inre av kvadraten, är värda 2 poäng. De linjesegment som går från ett hörn är värda 1 poäng. Övriga segment är värda noll poäng. Varje rektangel som ritas får nu ett poängvärde, nämligen summan av poängen för de linjesegment som ingår i rektangeln. Vi kan då konstatera att varje rektangel ger högst 8 poäng. De rektanglar som har antingen maximal bredd eller maximal höjd ger 8 poäng, medan alla andra rektanglar ger mindre. Det finns 9*4=36 stycken 2-poängskanter, och 8 stycken 1-poängskanter. Totalt finns det alltså 36*2 + 8 = 80 poäng. Eftersom varje ritad rektangel ger högst 8 poäng, krävs det alltså minst 10 rektanglar.
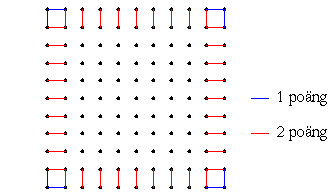
Vi kan nu undersöka om det är möjligt att hitta en lösning med bara 10 rektanglar. För att detta ska vara möjligt krävs dels att varje rektangel som används är en 8-poängare, dvs har antingen höjd eller bredd 10, dels att inga rektanglar överlappar varandra i ett poänggivande linjesegment. Om vi använder en 10x10-rektangel för att täcka de åtta 1-poängarna, kan vi sedan bara använda rektanglar som antingen täcker fyra horisontella 2-poängare, eller fyra vertikala 2-poängare. Eftersom det finns 18 av varje, och 18 inte är delbart med 4, går detta inte att åstadkomma. Om vi å andra sidan inte använder en 10x10-rektangel, måste vi täcka hörnen antingen med två rektanglar med bredd 10 och mindre höjd, eller med två rektanglar med höjd 10 och mindre bredd (allt annat ger antingen överlapp eller mindre än 8 poäng per rektangel). Då uppstår samma problem igen. Det återstår då antingen 14 horisontella 2-poängare och 18 vertikala, eller tvärtom. Eftersom de rektanglar vi kan använda bara kan täcka fyra 2-poängare på samma ledd, kan vi inte täcka de återstående linjesegmenten med ytterligare åtta rektanglar.
Eftersom det inte finns någon lösning med färre än tio rektanglar, och heller ingen med exakt tio, är elva rektanglar optimalt.
/Johan
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage