Majproblemen 2002
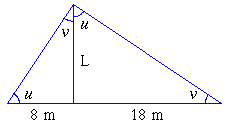
1. Solhöjden är solens vinkel över horisonten. Anna har en flaggstång i sin trädgård. En vacker dag mäter hon skuggan från flaggstången till 8 m vid solhöjden u. Senare samma dag är skuggan 18 m vid solhöjden v. Hon finner att u och v tillsammans är en rät vinkel. Hur lång är flaggstången? Bor Anna i Linköping?
2. Det är hög tid för matteläraren Svante att sätta betyg på eleverna Anders, Bodil, Carina, Daniel, Eija och Fredrik. Han väljer bland betygen G, VG och MVG och tänker dela ut minst ett betyg av varje slag. På hur många olika sätt kan han göra detta? Extrauppgift: Samma problem fast fler elever.
Lösningar
1. Låt L vara flaggstångens längd. Eftersom u och v har summan 90o så är de rätvinkliga trianglarna i figuren nedan likformiga. Det ger oss sambandet 8/L = L/18 eller ekvivalent L2 = 8*18 = 144. Dvs längden är 12 m.
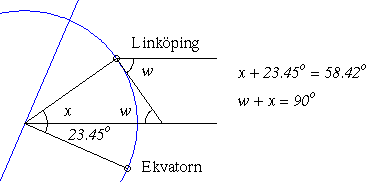
Bor Anna i Linköping? För solhöjden u gäller att tan(u) = 12/8, så att u = 56.31o. Låt w vara den högsta solhöjden i Linköping. Linköpings latitud (breddgrad) är 58.42o och solen står som högst vid midsommar då jordaxelns norra ände lutar 23.45o mot solen. Detta ger enligt figuren nedan
Anna bor alltså inte i Linköping utan längra söderut där solen står högre på himlen. Den som är intresserad av astronomi bör ta en titt på Lars Alexanderssons astronomiska almanackor.
/Jonas
2.
Metod I:
Det finns tre olika sätt betygen kan fördelas så att alla betyg delas ut: 2-2-2, dvs varje betyg ges till två personer, 3-2-1 och 4-1-1. Vi undersöker dessa i tur och ordning:
- 2-2-2
- Antalet kombinationer blir = (6*5/2) * (4*3)/2 = 90, eftersom betyget MVG kan ges till varje möjligt par, dvs 6*5/2 st. Kvar är 4 personer varav 2 ska få VG, det blir 4*3/2 möjligheter.
- 3-2-1
- Antag först att det är 3 G, 2 VG och 1 MVG. Det finns sex olika sådana fall, så resultatet ska sedan multipliceras med 6. 1 MVG kan ges till 6 personer, 2 VG till resterande 5 personer ger 5*4/2. Allt som allt blir det då: 6 * (6 * (5*4)/2) = 360 kombinationer
- 4-1-1
- Antag att det är 4 MVG. Då får vi 6 olika personer att ge den enda VG:n till och 5 kvar att dela ut G till. På samma sätt får vi 6*5 kombinationer om det finns 4 G eller 4 VG, så totalt får vi 3 * (6 * 5) = 90 kombinationer.
Sammantaget får vi alltså 90+360+90=540 olika sätt att dela ut betygen.
Metod II:
Vi börjar med alla kombinationer utan kravet att alla betyg ska delas ut, 36 st. Nu har vi räknat för mycket, så vi ska ta bort de fall där bara två eller ett betyg delats ut. G saknas i 26 fall, och samma för VG och MVG. Men nu har vi tagit bort fallet där bara G delats ut två gånger. När vi kompenserat för detta blir det 36 - 3 * 26 + 3*1 = 540 kombinationer.
Detta resonemang (kallat inklusion-exklusion) kan även användas då det finns fler elever. För n elever får vi 3n - 3 * 2n + 3 kombinationer.
/Erik
Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03
 Homepage
Homepage