Linköpings Universitet

Aprilproblemen 2002

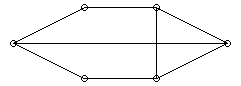
1. Flygbolaget Euroflop flyger mellan ett antal europeiska städer. Från varje stad har man direktförbindelser med högst tre andra städer. Om två städer saknar direktförbindelse kan man alltid flyga via en tredje stad. Bestäm det maximala antalet städer som Euroflop kan trafikera och rita en graf över hur flygtrafiken kan se ut. Nedan är en graf med sex städer, vilket inte är maximalt.

2. Fermats sista sats är mycket berömd och bevisades av Andrew Wiles så sent som 1994. Satsen säger att för ett heltal n > 2 finns det inte några positiva heltal x, y och z som löser ekvationen

xⁿ + yⁿ = zⁿ .

För vilka heltal n > 0 finns det positiva heltal x, y och z som löser den "omvända" ekvationen

n^x + n^y = n^z ?

---

Lösningar

1. Utgå från en stad A. Från A kan man ta direktflyg till högst tre andra städer. Dessa tre städer kan i sin tur ha direktflyg till ytterligare två städer var. Dvs från A kan man nå högst tre städer direkt och högst sex städer via en mellanlandning. Det betyder att grafen maximalt kan ha tio städer (noder).

Att det finns en graf med tio noder som uppfyller kraven visas nedan. Bilderna är olika vyer av en och samma graf, den så kallade petersengrafen.

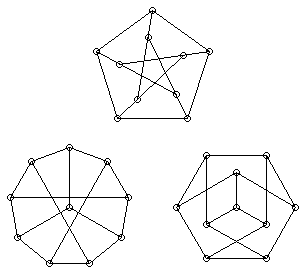
Notera att det inte finns någon graf med nio noder som uppfyller kraven. En graf med N noder och tre bågar (direktförbindelser) från varje nod har totalt 3*N/2 bågar. Det betyder att N måste vara jämn. En graf med udda antal noder (och högst tre bågar per nod) har därför någon nod med högst två bågar. Från en sådan nod kan man nå högst två noder direkt och högst fyra noder via en mellanlandning. Dvs grafen har högst sju noder.

/Jonas

---

2. Antag att x, y och z är positiva heltal som löser ekvationen

n^x + n^y = n^z .

Då måste var och en av termerna n^x och n^y vara mindre än n^z, det vill säga exponenterna x och y måste vara mindre än z. Dessutom måste n vara större än 1. Om n > 2, är var och en av termerna n^x och n^y mindre än hälften av n^z, vilket gör ekvationen omöjlig. Således måste n vara lika med 2.

Eftersom termerna 2^x och 2^y är högst hälften av 2^z, är enda möjligheten att båda termerna är precis hälften av 2^z. Vi måste då ha x = y = z - 1. Samtliga lösningar till ekvationen har därför formen

2^x + 2^x = 2^{x + 1} .

Situationen är alltså lustigt nog densamma som för Fermats ekvation: För n = 2 finns oändligt många lösningar, men för n > 2 finns inga lösningar. Fermats problem var dock något svårare.

/Johan

Sidansvarig: jana.bjorn@liu.se
Senast uppdaterad: 2019-12-03